除算アルゴリズム

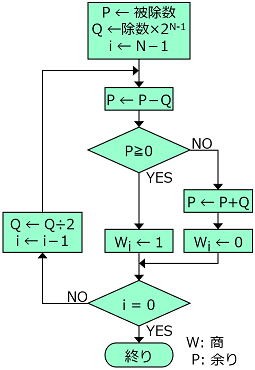
■復元法

除算のアルゴリズムは、人間が筆算で行う除算と同じである。 すなわち、桁を合わせながら除数と被除数を比較し、除数が被除数以下ならば商にビット1を立てるとともに被除数から除数を引く(引き算を行う)。 除数が被除数より大きければ商にビット0を立て、引き算は行わない。

除数と被除数の大小関係は、比較演算を行って調べても良いが、まず減算を行って結果の符号で判定する方法もある。 すなわち、まず被除数から除数を引く。結果が正または0ならば、除数が被除数以下であることを意味するので、商にビット1を立てる。 引き算の結果が負ならば、除数が被除数よりも大きいことを意味するので、商にビット0を立てる。このとき、実際には引き算を行ってはならないのだから、除数を加え戻す。 この方法に基づく除算アルゴリズムを復元法(Restoring method)と呼ぶ。

■非復元法

復元法において被除数(P)から除数(Q)を引いた結果であるP-Qの符号を調べ、負ならば除数(Q)を加え戻す。 そして、次の繰り返しでは除数を半分にしたQ/2を被除数から引いた結果P-Q/2の符号を調べる。

ここで、被除数(P)から除数(Q)を引いた結果P-Qが負の場合に、除数(Q)の加え戻しを行わないとする。このとき、次の繰り返しでは除数を半分にしたQ/2を被除数から引くのではなく加えるとする。

これは、(P-Q)+Q/2=P-Q/2を求めたことになり、加え戻し後にQ/2を引いた結果に等しい。 このように、被除数と除数の間の演算を減算と加算で切替えることで、加え戻し(被除数復元)のための演算を省略することができる。

この除算手法を非復元法(Non-restoring method)と呼ぶ。

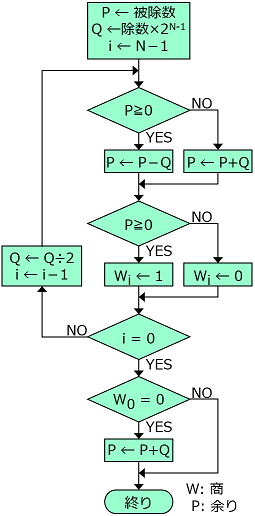
非復元法に基づいた、 除数、非除数とも符号無しの場合の除算アルゴリズムを以下の図に示す。

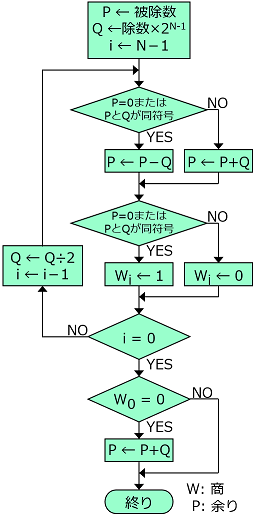
除数、非除数とも符号付きの場合には、除数、非除数の符号判定の部分が変更になるだけで、基本的に除算アルゴリズムは変化しない。符号付きの場合の非復元法除算アルゴリズムを以下の図に示す。